Flowchart
Seperti telah dijelaskan pada bab sebelumnya bahwa flowchart
digunakan untuk menggambarkan algoritma atau proses. Flowchart disusun
menggunakan simbol-simbol, maka dapat memberikan gambaran yang efektif
dan jelas tentang prosedur logika.
Dalam hal melakukan koreksi atau analisis dari suatu permasalahan,
flowchart dapat dengan mudah untuk dilihat dan dikomunikasikan. Hal ini
dikarenakan flowchart disusun atas simbol-simbol yang mengikuti suatu
standar tertentu.
Pengambilan Keputusan
Pengambilan keputusan perlu dilakukan apabila harus menentukan
satu pilihan dari (minimal) dua pilihan yang ada. Dalam hal mengambil
keputusan, perlu diketahui kondisi yang sedang dihadapi. Kondisi ini bisa berupa
pernyataan boolean atau proses perbandingan. Dalam flowchart, simbol yang
digunakan untuk pengambilan keputusan adalah berbentuk belah ketupat.
Simbol pengambilan keputusan hanya memiliki satu buah input dan dua buah
output yang digunakan untuk memfasilitasi hasil dari pengujian kondisi, yaitu
“Ya” atau “Tidak”, “True” atau “False”.
Dalam melakukan pengujian kondisi, terdapat beberapa notasi yang
dapat digunakan, misalnya menggunakan notasi relasional berikut :
TABEL NOT X
Seperti telah dijelaskan pada bab sebelumnya bahwa flowchart
digunakan untuk menggambarkan algoritma atau proses. Flowchart disusun
menggunakan simbol-simbol, maka dapat memberikan gambaran yang efektif
dan jelas tentang prosedur logika.
Dalam hal melakukan koreksi atau analisis dari suatu permasalahan,
flowchart dapat dengan mudah untuk dilihat dan dikomunikasikan. Hal ini
dikarenakan flowchart disusun atas simbol-simbol yang mengikuti suatu
standar tertentu.
Pengambilan Keputusan
Pengambilan keputusan perlu dilakukan apabila harus menentukan
satu pilihan dari (minimal) dua pilihan yang ada. Dalam hal mengambil
keputusan, perlu diketahui kondisi yang sedang dihadapi. Kondisi ini bisa berupa
pernyataan boolean atau proses perbandingan. Dalam flowchart, simbol yang
digunakan untuk pengambilan keputusan adalah berbentuk belah ketupat.
Simbol pengambilan keputusan hanya memiliki satu buah input dan dua buah
output yang digunakan untuk memfasilitasi hasil dari pengujian kondisi, yaitu
“Ya” atau “Tidak”, “True” atau “False”.
Dalam melakukan pengujian kondisi, terdapat beberapa notasi yang
dapat digunakan, misalnya menggunakan notasi relasional berikut :
>
|
Lebih
besar dari
|
<
|
Kurang
dari
|
≥
|
Lebih
besar atau sama dengan
|
≤
|
Kurang
dari atau sama dengan
|
< >
|
Tidak
sama dengan
|
Dalam proses pengambilan keputusan, kadang kala terdapat
beberapa syarat sekaligus. Untuk menangani hal ini dapat digunakan ekspresi
aljabar boolean. Aljabar boolean merupakan kalkulus logika yang digunakan
untuk menentukan nilai kebenaran dari suatu ekspresi logika [10]. Teknik
aljabar ini dikembangkan oleh George Boole pada tahun 1930an, sebagai
penghargaan atas penemuannya maka aljabar ini diberi nama sesuai dengan
nama belakang beliau.
Dalam aljabar boolean terdapat tiga buah operasi dasar, yaitu : AND,
OR, NOT ketiga-tiganya dapat digunakan secara independen atau dapat
digunakan sekaligus. Keluaran (output) dari aljabar ini adalah nilai benar
(TRUE) atau salah (FALSE).
Berikut ini adalah tabel yang menunjukkan ketiga hasil operasi aljabar
boolean :
TABEL X AND Y
X
|
Y
|
X AND
Y
|
T
|
T
|
T
|
T
|
F
|
F
|
F
|
T
|
F
|
F
|
F
|
F
|
TABEL X AND OR
X
|
Y
|
X AND
OR
|
T
|
T
|
T
|
T
|
F
|
T
|
F
|
T
|
T
|
F
|
F
|
F
|
TABEL NOT X
X
|
NOT X
|
T
|
F
|
F
|
T
|
Pengulangan Proses
Dalam beberapa kasus, seringkali terdapat proses yang harus dilakukan
secara berulang-ulang, sebagai contoh yang paling sederhana adalah proses
berjalan kaki. Untuk bisa mencapai tujuan, kita harus melangkahkan kaki
secara berulang-ulang supaya dapat menempuh jarak tertentu dan akhirnya
sampai tujuan.
Pada kasus yang berhubungan dengan pengolahan informasi
menggunakan komputer, terdapat proses-proses yang harus dilakukan secara
berulang, mulai dari input data, proses dan output. Program yang baik adalah
program yang bisa mengoptimalkan kinerja komputer, dengan cara
menggunakan kembali program atau sekumpulan program dengan proses
tertentu. Atau dengan kata lain terdapat bagian program yang dapat
dipanggil/digunakan secara berulang-ulang. Hal ini akan mempermudah
pekerjaan programmer dalam menghasilkan solusi.
Contoh:
Seorang staff IT diminta untuk menampilkan data dari sebuah tabel dimana di
dalamnya terdapat seratus baris data. Jika staff tersebut harus menampilkan
satu per satu, tentunya akan membutuhkan banyak kode program dan program
akan menjadi tidak efektif.
Solusi:
Dalam kasus ini yang diminta adalah bagaimana menampilkan data sebanyak
100 baris tanpa harus menggunakan proses output sebanyak 100 kali. Metode
yang digunakan adalah pengulangan.
Dalam proses pengulangan terdapat 3 (tiga) hal penting, yaitu:
1. Inisialisasi (penentuan kondisi/nilai awal)
2. Proses
3. Kondisi berhenti
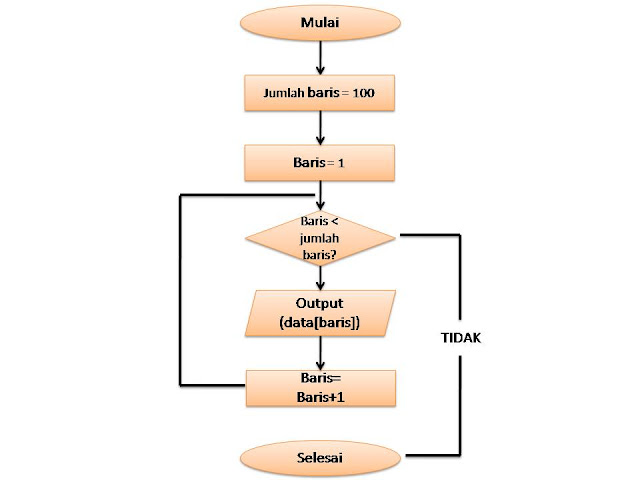
Untuk kasus menampilkan data, dapat ditentukan bahwa jumlah baris yang akan
dibaca adalah 100. Baris akan dibaca mulai dari baris pertama (baris = 1). Proses
yang dilakukan adalah membaca dan menampilkan isinya ke layar (output).Pembacaan akan berhenti jika baris yang dibaca sudah mencapai baris ke-100 Jika digambarkan menggunakan flowchart maka, akan tampak sebagai berikut:
Pseudocode
Pada bab 1 telah dijelaskan sebelumnya mengenai keuntungan dalam
menuangkan logika dan algoritma menggunakan pseudocode. Dalam
menyelesaikan kasus yang besar dan kompleks, misalnya membuat aplikasi
untuk menangani proses bisnis sebuah perusahaan maka, yang paling cocok
digunakan dalam menuliskan algoritma adalah pseudocode.
Sesungguhnya tidak ada aturan baku dalam penulisan pseudocode,
namun karena banyaknya bahasa pemrograman yang beredar saat ini maka,
aturan penulisan pseudocode diarahkan untuk menyerupai aturan penulisan
bahasa pemroraman tertentu. Dalam buku ini akan digunakan aturan
penulisan pseudocode yang mendekati bahasa pemrograman Pascal.
Struktur algoritma
Struktur algoritma yang digunakan mengacu pada struktur
pemrograman bahasa Pascal yang terdiri dari 3 (tiga) bagian, yaitu :
- Judul
- Deklarasi/Kamus Data
- Badan Program
Pada bagian judul, digunakan sebagai tempat untuk mencantumkan
nama atau judul program. Terdapat aturan penulisan judul, yakni:
1. Tidak diawali dengan angka atau karakter selain alphabet
2. Tidak terdapat karakter spasi atau karakter selain alphabet
kecuali karakter underscore ‘_’ (sebagai pengganti karakter
spasi).
Contoh
Algoritma menghitung;
|
BENAR
|
Algoritma konversi bilangan;
|
SALAH
|
Algoritma perhitungan_pajak;
|
BENAR
|
Algoritma 2 bilangan;
|
SALAH
|
Algoritma *kecil;
|
SALAH
|
Pada bagian deklarasi, digunakan sebagai tempat untuk
mencantumkan variabel, konstanta, dan record. Mengingat cara eksekusi kode
program dilakukan berurut dari atas ke bawah maka, deklarasi diletakkan di
awal program setelah bagian judul. Hal-hal yang dideklarasikan pada bagian ini
digunakan sebagai ‘reservasi’ alokasi memory untuk penyimpanan data dan
akan digunakan selama program bekerja.
Pada bahasa pemrograman Pascal, bagian deklarasi juga berfungsi
untuk mendeklarasikan nama function dan procedure.
Contoh:
Algoritma Coba;
Kamus data
x : integer;
s : string;
...
Pada bagian badan program, digunakan untuk meletakkan semua
algoritma atau kode-kode program. Bagian ini diawali dengan ‘BEGIN’ dan
diakhiri dengan ‘END’. Semua algoritma atau kode program wajib dituliskan
diantara kedua penanda tersebut.
Contoh:
Algoritma Hello
Kamus data
s : string
BEGIN ← Tanda awal Algoritma
s ⇦“Halo!”
output(s)
END.← Tanda akhir Algoritma
Input dan Output
Dalam mengawali suatu proses tertentu, minimal membutuhkan suatu
masukan berupa data (input), karena data inilah yang nantinya akan diproses
dan akan menjadi keluaran (output).
Contoh :
Menerima masukan data dari user (pengguna)
Algoritma
Masukkan_data
Kamus data
BEGIN
input(x) /*x
adalah variabel penampung nilai*/
END.
|
Memasukkan nilai tertentu pada variabel
Algoritma
Masukkan_nilai
Kamus data
BEGIN
x ← 5
/*panah ke kiri arah masuknya nilai*/
END.
|
Menampilkan isi variabel ke layar monitor
Algoritma
Tampilan
Kamus data
BEGIN
output(x) /*x
adalah variabel yang berisi nilai*/
END.
|